円周率とは?
円周率という言葉は聞いたことがあるかな?
さすがにあるよ!馬鹿にしないでよね!?
では、円周率とは何を指しているのか、説明してくれたまへ。
・・・円の周りの長さとか面積を求めるのに使うアレでしょ?$3.14\cdots$みたいな感じの。
・・・今日はそんな人のために説明しよう。
円周率とは?
円の直径に対する円周(円の周囲の長さ)の割合を表したモノが円周率だ。なので、直径に円周率を掛けると、円周が得られる。例えば、直径$1$mの円があったとすると、円周は約$3.14$mとなる訳だ。
つまり直径の3.14倍が円周ってことでしょ?なんだ、大体あってるじゃん。
円周や面積を求めるだけが、円周率の役割とは言えない。説明としては不完全だよ、チミ。あと3.14が許されるのは小学生までだ。
円周率は「循環しない無限小数」なので、省略せずに正確に表すことは無理だ。なので記号$\pi$(パイ)を用いて表す。
なら直径1mの円なら、$\pi$m(パイメートル)ってこと?なんかキモいなぁ。
一々、「約3.14」とか「3.14・・・」とか用いなくても、円周率を一文字で正確に表現出来るのだ。なかなか便利だろう?
円の形はどれも同じだから、違う大きさの円でも円周率は使える。なので1mの円周が$\pi$mなら、5mの円周は?
$5 \pi$mってことね!
なぜ円周率は3.14・・・?
実際に測って求める
はい、質問!円周率の3.14ナントカカントカって数字はどこからやって来たの?どうやって調べたの?
別に実際に測って調べることも出来るぞ。
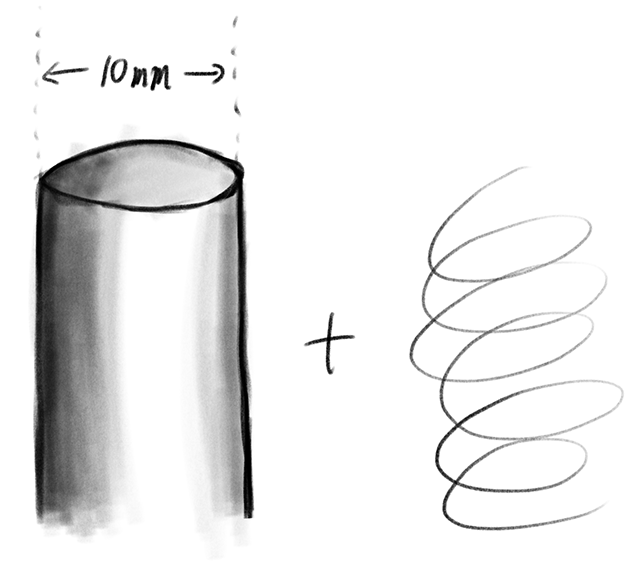
直径10mm(100mmもいいが高いぞ)の円柱と印を付けられる糸をホームセンターなどで買ってきたまへ。出来る限り正確な円柱を見つけてくるのだよ。あとは油性ペンと物差しも用意しておくように。
1時間後・・・。
とりあえず直径10mmのステンレスの棒が売ってたから、買ってきたよ!あと裁縫用の白糸が余ってたから、これ使えないかな?
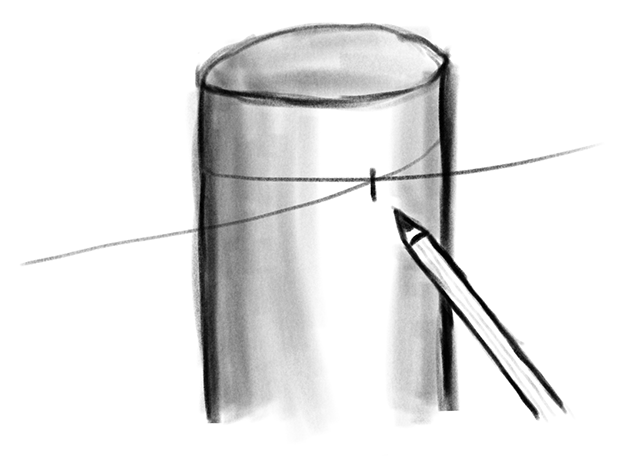
よろしい、じゃあ糸を円柱に巻き付けて、油性ペンで糸に印を付けよう。
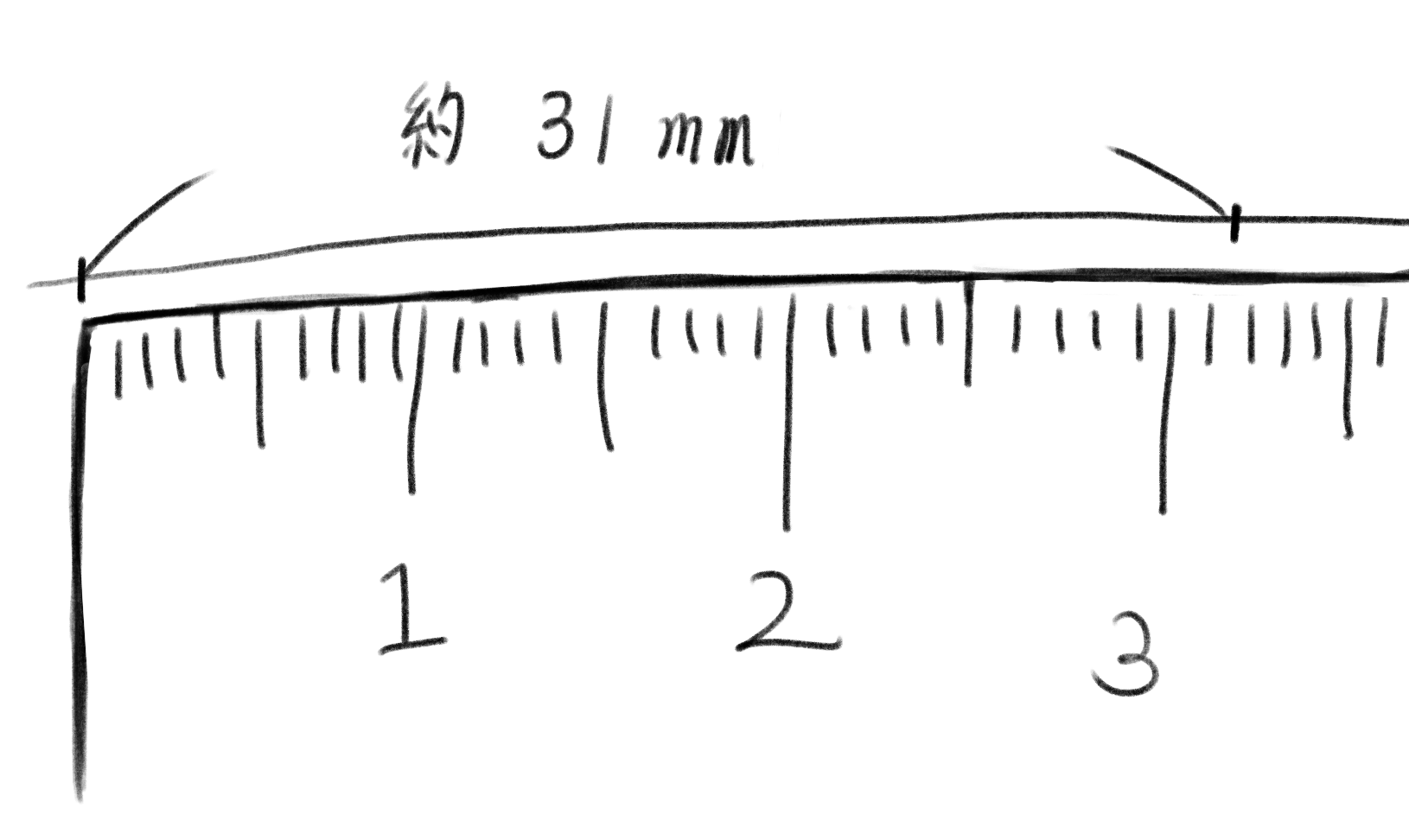
あとは印を付けたところの長さを測れば、円周を測ることが出来る。だいたい3.1cm=31mmになっていることが確認できるだろう。
確かに31mmくらいになってる!すごーい!
計算で求める
何をやっているのかと思って来てみれば、またアナログなことをしているのデスナ。
体感するのも数学の醍醐味だからな。大事なことだ。別の求め方についても紹介しよう。ロボット君も手伝ってくれ。
このような図について考えて見よう。まず直径1(cmでもmでもkmでもいいぞ)の円を描く。その円の内側にピッタリと収まる三角形を描く(円に内接すると言う)。そして、こんどは円が内側にピッタリ収まるような三角形を描く(円に外接すると言う)。さて、内接する三角形の外周と外接する三角形の外周、そして円周の長さを長い順に言ってくれたまへ。
外側の三角形が一番大きいから、周りの長さも一番長いはずだわ。その次が円で、内側の三角形が一番短いはず・・・。どうよ!
まぁそうだな。じゃあ、この三角形を四角形にしてみよう。上の図のレバーを右に動かしてみたまへ。
すごい、四角形になった!
そのまま、どんどん右へずらしてみよう。
(パソコンを使っている人はスライダーをクリックしてから、キーボードのカーソルキー「→」で一個ずつ動かせマスヨ。)
内側と外側の図形が、どんどん円に近づいていく!
図の左上にある数値に着目してくれ。変化する過程で円周は「外接する多角形の周囲」と「内接する多角形の周囲」の間にある長さというのが、分かるだろう。どんどん角を増やしていけば、より正確な円周率を特定することが出来るのだ!
おもしろーい!このまま一万角形位までやらせてよ!
それはワタシの演算能力に大変負荷が掛かるので、お断りシマス!
| 多角形の辺の数 | 内接する多角形の外周 | 外接する多角形の外周 |
|---|---|---|
| 3 | 2.598076211 | 5.196152423 |
| 4 | 2.828427125 | 4 |
| 5 | 2.938926261 | 3.63271264 |
| 6 | 3 | 3.464101615 |
| 7 | 3.037186174 | 3.371022332 |
| 8 | 3.061467459 | 3.313708499 |
| 9 | 3.07818129 | 3.275732108 |
| 10 | 3.090169944 | 3.249196962 |
| 100 | 3.141075908 | 3.142626604 |
| 1000 | 3.141587486 | 3.141602989 |
| 10000 | 3.141592602 | 3.141592757 |
| 100000 | 3.141592653 | 3.141592655 |
| 1000000 | 3.141592654 | 3.141592654 |
確かにこれは効率の悪い方法だ。10万角形でも小数第8位(3.14159265)までしか絞り込めない。このまま続けるとロボット君がフリーズしてしまうだろう。実は世の中にはもっと効率のよい円周率の求め方がある。
それは?
続きはWebにあるから、自分で探してくるのだ。
全部、ぶん投げたー!
(・・・ココも一応Webなのでは?)