いろいろアップデートされた
27日はプロトタイプガンダムとゲルググ(量産型)のガチャ追加、今日28日は待っていた人も多かっただろう、調査部隊のコンテナが実装された。
2018.09.28アップデートファイル ver.0104 の配信
追加されたMS等
無課金プレイだとなかなかMSが揃わないけど、今回は運良くプロトタイプガンダムLv1が引けた。
350コストからだが、今日から250~650までのコスト制限部屋が解禁されたため、十分実用的。
BDがLv2の400コストだから、ちょうどいい感じではある。
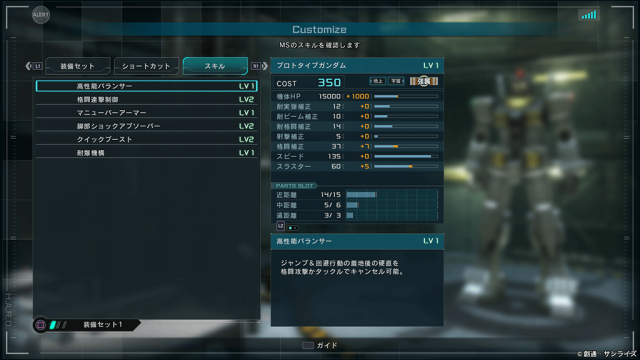
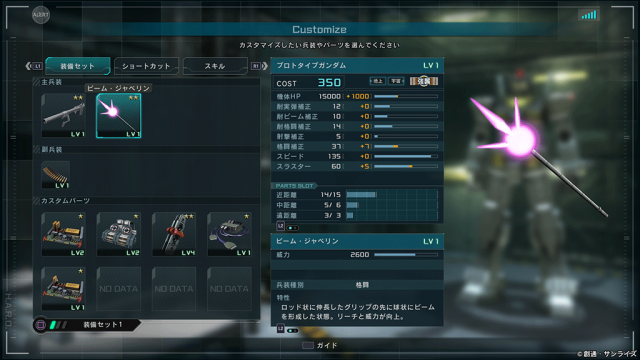
肝心のプロガンだけど、
- 高火力のジャベリンorビームサーベル*2
- バズ装備可能
- 高耐久
- 必要十分の機動力
と、今までの強襲機をほとんど食べちゃった感じに高水準でバランスが取れた機体。
これからは単機で支援機を狩れる爆発力のEXAMと、前線維持可能な安定志向のプロガンの2択となりそう。
G3の居場所がこれで完全になくなった気がするんだが。
元からなかったとか言わないように。
このインフレ感漂う機体HPは、今後の強襲機の調整を見越しての数値なのだろうか、そう信じたい。
ジムストライカーは泣いていいと思う。
ゲルググ(量産型)は現状ビームライフルしか装備できない模様。
コスト350スタート以外で、武器がこれでは価値を見出すのが難しそう。
今後の武器の追加に期待。
ガンダムピクシーLv1も実は当たってたが、個人的にあまり欲しくなかった。
ステルス、高火力、低耐久、低機動と、とにかくすぐに落ちやすい。
ぶっちゃけ高性能版アッガイなのだが、EXAMかプロガンで良さそう。
上手い人が使えば~と聞くが、上手い人はEXAMやプロガン乗るともっと手に負えない感じ。
実に短命だった、合掌。
イフリートLv1も当たった、むしろこれはアリ。
ショットガンによる近距離戦の強さが尋常じゃないほど強く、マニューバもこれで止まる。
弾数3発であるのとリロードの遅さから、継戦能力の低さが気になるところ。
ジャイアントバズも持てるので、MAPや編成によっては変更して対応出来る点も素晴らしい。
ゲームバランス調整も行うと発表があったので、産業廃棄物と化している機体や装備を何とか救ってもらいたい。
その他
「250」、「350」、「450」、「550」、「650」のコスト制限部屋が作成可能になり、レーティングマッチやクイックでも50端数のものが出てきた。
今までハズレ扱いだったレベルの機体が出せるので、これはありがたい。
が、ジムコマンドが高性能過ぎて、350以下汎用はジムコマンド一強状態。
調整を待つほかない。
クイックマッチにフレンドが呼べるようになった。
先にクイックマッチにてプライベートルームを建てて、フレンドを呼んでから解除するようだ。
なので既に建っているクイックマッチのルームに呼ぶことは出来ない模様。
クイックが現状人気がないので人が集まるか不安ではあるが。
しゃがみによる「よろけ無効」がなくなった。
見合った時にお互いにしゃがむ様は、あまり格好良くなかったものの、近距離の選択肢が減ってしまったのは残念である。
これでいよいよ緊急回避スキルの有無が大きくなった。
なおタンクには「機体固定装置」なる新スキルが付与された。
タンクのステータスそのものの上方修正はまだみたいだが。
「本日の任務状況」ということで、終わってない項目を一目で確認出来るようになったのは助かる。
気になったのはこれくらい。
後1、2回くらいアップデートしたら、かなり良くなりそうな予感がしてきた。
ただガチャだけは、最初から根本的に失敗していると思うけど。
まだまだバトオペは無課金で頑張る。