なぜ数学を学ぶのか
数学って必要なの?式の意味が分からないし、計算が大変だし。何で勉強するのか理由が分からない。
ナルホド。では専門家に聞いてみまショウ。こちらへドウゾ。
ちぃーす。
え、何このネズミは?
はじめに
それはこちらの台詞だ。モノを教わる人間の態度とは思えんよチミ。
なんかごめんなさい。
ヒソヒソ・・・(なんでアンタが教えてくれないの?)
ピピピ・・・(ワタシはロボットナノデ、数学に関する知識は最初からインプットされてマス。数学を知らない人間の気持ちは全く理解出来ませんので依頼シマシタ。)
ヒソヒソ・・・(なんか腹立つ言い方だなぁ。)
コラ、私語は慎みたまえ!
曽呂利新左衛門のお話
では今日は「曽呂利新左衛門」の話でもしよう。
そろ・・・なんだって?
「曽呂利新左衛門(そろりしんざえもん)」デス。戦国時代で豊臣秀吉に仕えていて、刀の鞘を作っていた人物デス。落語の始祖としても有名だったそうデス。
彼について、こう言う民話が知られている。

病で寝込んでいる豊臣秀吉だが、大事にしていた盆栽の松の木が枯れてしまって、余計に落ち込んでいた。すると曽呂利新左衛門は歌を詠んで、松の木は秀吉の代わりに枯れたのだと励ました。
喜んだ秀吉は新左衛門に褒美を取らせたいと言った。新左衛門は「1ヶ月の間、毎日1文倍増し」貰えれば結構だと。秀吉に1文倍増しの意味について訪ねられると、「1日目は1文、2日目は2文、3日目は4文という風に日ごとに倍ずつ増える」という意味らしい。秀吉は無欲な奴だと思い、会計に新左衛門の言うとおり1文倍増しで渡すように命じた。
曽呂利新左衛門(そろりしんざえもん)- 山形県の昔話 – 民話の部屋 | フジパン
ちなみに1文って今だといくらくらいなの?
50円くらいのようデスネ。
せっかく天下人から褒美が貰えるのに、新左衛門は欲がないんだね。
(ニヤニヤ)さて、それはどうだろう?早速、式にしてみよう。
「1日目は1文、2日目は2文、3日目は4文・・・」と増えていくから、倍にして順に足していけば良い。
$\begin{align*} 1 &+ \\ 2 &+ \\ 4 &+ \\ 8 &+ \\ 16 &+ \\ 32 &+ \\ 64 &+ \\ 128 &+ \\ 256 &+ \\ 512 &+ \\ 1024 &+ \\ 2048 &+ \\ 4096 &+ \\ 8192 &+ \\ 16384 &+ \\ 32768 &+ \\ 65536 &+ \\ \cdots \end{align*}$
ちょ、ちょっと待った!数字がすごいことになってるけど!!
1日倍ずつ増えていきますカラ、これで正しいデス。ちなみに65536文は17日目に貰える額デス。
げえぇぇーーー!じゃあ約束の30日後には一体いくらに?
$\begin{align*}
1 &+ \\ 2 &+ \\ 4 &+ \\ 8 &+ \\ 16 &+ \\ 32 &+ \\ 64 &+ \\ 128 &+ \\ 256 &+ \\ 512 &+ \\ 1024 &+ \\ 2048 &+ \\ 4096 &+ \\ 8192 &+ \\ 16384 &+ \\ 32768 &+ \\ 65536 &+ \\ 131072 &+ \\ 262144 &+ \\ 524288 &+ \\ 1048576 &+ \\ 2097152 &+ \\ 4194304 &+ \\ 8388608 &+ \\ 16777216 &+ \\ 33554432 &+ \\ 67108864 &+ \\ 134217728 &+ \\ 268435456 &+ \\ 536870912 &= 1073741823
\end{align*}$
1,073,741,823文だな。さて先ほど言っていた通り、一文50円とすると現代価値ではいくらになる?電卓を使って良いから計算してみるといい。
ポチポチ・・・($1073741823 \times 50 = 53687091150$)
ええと、一、十、百、千、万、十万、百万、千万、一億、十億、百億・・・。536億円!?新左衛門って強欲過ぎるかも・・・!
騙される方が悪い。ちょっと考えれば分かる話だが、数学が出来ないとその発想に至らないわけだ。数学とは「思考の道具」なのだ。
推論の道具としての数学
もしも秀吉が等比数列について知っていたり、知らなかったとしても実際に計算してみたら、この話には引っ掛からなかっただろう。
等比数列?何それ?
こういう書き方をしてみようか。
$\begin{align*}&1+2+4+8+16+ \cdots \\
&= 1 + (1 \times 2) + (1 \times 2 \times 2) + (1 \times 2 \times 2 \times 2) + (1 \times 2 \times 2 \times 2 \times 2)\end{align*}$
う、数式を見ているだけで段々気持ちが悪く・・・エロエロエロオオォォ・・・。
口からエクトプラズム出てマスヨ。耐性が低すぎデス。
1日目は1文からだが、2日目は1文の倍、3日目は1文の倍の倍、4日目は1文の倍の倍の倍・・・なので、それを式で表した。ようは、「計算する前の形」に戻しただけだ。
| ○日目 | その日に受け取る金額 | 式1 | 式2 | 日本語 | ||
| $\textcolor{red}1$ | $1$ | $=$ | $1$ | $=$ | $1$ | 1文 |
| $\textcolor{red}2$ | $2$ | $=$ | $1 \times 2$ | $=$ | $1 \times 2^\textcolor{red}1$ | 1文の倍 |
| $\textcolor{red}3$ | $4$ | $=$ | $1 \times 2 \times 2$ | $=$ | $1 \times 2^\textcolor{red}2$ | 1文の倍の倍 |
| $\textcolor{red}4$ | $8$ | $=$ | $1 \times 2 \times 2 \times 2$ | $=$ | $1 \times 2^\textcolor{red}3$ | 1文の倍の倍の倍 |
| $\textcolor{red}5$ | $16$ | $=$ | $1 \times 2 \times 2 \times 2 \times 2$ | $=$ | $1 \times 2^\textcolor{red}4$ | 1文の倍の倍の倍の倍 |
式でわかりにくいなら、表にしてみると良いかもしれん。
確かに毎日「倍ずつ」増やして欲しいって新左衛門も言ってるから、「$\times 2$」が増えていくのは分かるわ。
$2 \times 2 \times 2 = 2^3$のように指数を用いて表せば、「$\times 2$」されている数がよく分かる。それが式2だ。
上の表1で「日数」と「式2の指数部(2の右上の小さな数字)」が何か関係しているように見えないか?
日数から1減った数と一致してるね。でも1日目はまだ倍になっていないから、そこだけ違うけど。
その通り。ちなみに1日目は$1 = 1 \times 2^0$と表現すれば、綺麗に表現出来る。
| 日数 | 金額 | 式2 | 式3 | |
| $\textcolor{red}1$ | 1 | $1 \times 2^\bf 0$ | $=$ | $2^{( \textcolor{red}1-1)}$ |
| $\textcolor{red}2$ | 2 | $1 \times 2^\bf 1$ | $=$ | $2^{(\textcolor{red}2-1)}$ |
| $\textcolor{red}3$ | 4 | $1 \times 2^\bf 2$ | $=$ | $2^{(\textcolor{red}3-1)}$ |
| $\textcolor{red}4$ | 8 | $1 \times 2^\bf 3$ | $=$ | $2^{(\textcolor{red}4-1)}$ |
| $\textcolor{red}5$ | 16 | $1 \times 2^\bf 4$ | $=$ | $2^{(\textcolor{red}5-1)}$ |
指摘の通り、表2の「式2」では「2の指数部が日数より1少ない」状態だ。なので「式3」のように1日目は「$0=1-1$」、2日目であれば「$1=2-1$」と書き換えてやれば、「日数$-1$」と表現出来る。ついでに「$1 \times$」も省略しよう。1を掛けても値はまったく変わらない。
式3に書き直すのに意味はあるの?
例えば、新左衛門が30日目に貰える額がスグに計算出来る。2日目に$2^{(\textcolor{red}2-1)}$、3日目に$2^{(\textcolor{red}3-1)}$だから・・・
30日目には$2^{(\textcolor{red}{30}-1)}=2^{29}$ってことね!つまり2を29回掛けた数が貰える金額になるのね。
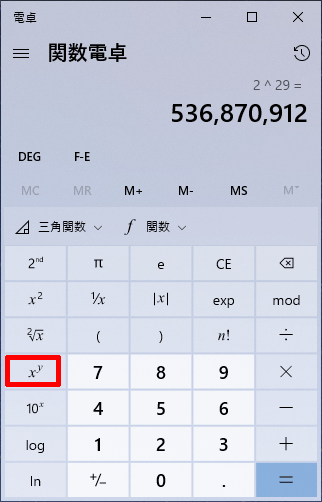
やれば出来るじゃねーか。ちなみに関数電卓を使えば、$2^{29}$はスグに計算出来るぞ。
Windows10に標準で搭載されている電卓も、関数電卓機能が備わっていますので、試してみてはいかがデショウカ?

日数を$n$に置き換えて、一般化してみよう!
一般化・・・?
$2^{(\textcolor{red}{30}-1)}=2^{29}$は30日の貰える金額しか表すことが出来ない特殊な例だが、日数を$n$に置き換えると、$n$に好きな日数を入れることでいろんな日数の金額を求めることが出来る。これを一般化と呼んでいる訳だ。
つまり使いやすくしているだけデスネ。
$\begin{align*}
日数を&n,そのn日目に貰える額をa_nとすると,\\
a_n & = 2^{(n – 1)}
\end{align*}$
数式を用いて具体的に計算してみることで、問題を整理して簡潔にし分かりやすくすることが出来る。つまりある事柄を予想し、問題の理解を深めることに大いに役立つわけだ。
最初の足し算の方が、深く考えなくて分かりやすい気がするのだけど。
理解に至れば、一々先頭から足していくのはクソ面倒くさいと思えるし、計算途中で間違える可能性も減らせる。
・・・なるほど、分かった(気がする)!
言語としての数学
一方で、「1日目は1文、2日目は2文、3日目は4文・・・」とだけ聞くと、一件大したことのないように思えるが、4日目以降の省略された部分が大事だったことが分かるだろう。
最初だけ聞くと、新左衛門は控えめな人だと思うわ。
しかし貰える合計金額、つまり総和は「等比数列の和の公式」を用いてこう表される。
$\begin{align*}
日数を&n,総額をS_nとすると,\\
S_n &= \cfrac{1 \times (2^n -1)}{2-1} = 2^n – 1
\end{align*}$
・・・え、どっから沸いて出てきたの、これ。
ページの都合上、ここでは公式の導き方は解説しない。$n$に日数を代入(数字と入れ替える)すれば、正しいことが分かるだろう。
確かに5日後なら$1+2+4+8+16=31$、上の式なら$2^\textcolor{red}5 – 1 = 31$で、一緒になるわ。すごーい。
では日本語、足し算、等比数列の和と3種類で表現してみるぞ。
【日本語】
「1日目は1文,2日目は2文,3日目は4文,4日目は8文,5日目は16文,6日目は32文,7日目は64文,8日目は128文,9日目は256文,10日目は512文,11日目は1,024文,12日目は2,048文,13日目は4,096文,14日目は8,192文,15日目は16,384文,16日目は32,768文,17日目は65,536文,18日目は131,072文,19日目は262,144文,20日目は524,288文,21日目は1,048,576文,22日目は2,097,152文,23日目は4,194,304文,24日目は8,388,608文,25日目は16,777,216文,26日目は33,554,432文,27日目は67,108,864文,28日目は134,217,728文,29日目は268,435,456文,30日目は536,870,912文の総和は1,073,741,823文」
【足し算】
$\begin{align*}
1 &+ \\ 2 &+ \\ 4 &+ \\ 8 &+ \\ 16 &+ \\ 32 &+ \\ 64 &+ \\ 128 &+ \\ 256 &+ \\ 512 &+ \\ 1024 &+ \\ 2048 &+ \\ 4096 &+ \\ 8192 &+ \\ 16384 &+ \\ 32768 &+ \\ 655366 &+ \\ 131072 &+ \\ 262144 &+ \\ 524288 &+ \\ 1048576 &+ \\ 2097152 &+ \\ 4194304 &+ \\ 8388608 &+ \\ 16777216 &+ \\ 33554432 &+ \\ 67108864 &+ \\ 134217728 &+ \\ 268435456 &+ \\ 536870912 &= 1073741823
\end{align*}$
【等比数列の和の公式】
$\begin{align*}
日数を&n,n日までに貰える総額をS_nとすると,\\
S_n &= \cfrac{1 \times (2^n -1)}{2-1} = 2^n – 1\\
\therefore 2^{30} – 1 &= 1073741823
\end{align*}$
このように並べてみると、数学の言語としての優秀さが伝わるだろう。かなり簡潔に表せる。また数式部分は万国共通で、日本語が分からなくとも内容が伝わりやすい。
確かに書く量は減るし、読む量も減る。でも式自体は苦手だけど。
英語が読めない人が、英文を見たときと同じだ。単語を知らないし、文法を理解していないから分からない読めない。だから苦手なのだ。
私でも数学が使えるようになるかな?
・・・やる気がないのは、教えるのが上手い人でも無理だ。ただ、やる気が続くなら大丈夫だ。絶対に出来るようになるぞ。
まとめ
サテ、いかがだったデショウカ?
ちょっと数学をやりたくなってきたよ。ちょっと口悪いけど案外良い奴じゃん、ネズミ。
誉めても何も出んぞ。
数学は普段の生活で様々なところで使われている。時間と暦の影響を受けない人なんていない。社会で生きていく以上、お金も使う。数学を学ばないということは、自然や科学、社会の仕組みや構造を知ることの放棄だと言って良い。
でも数学出来なくても生きていけるよ。算数が出来ればお金の計算は出来るし、時計だって読めるよ。仕事だっていくらでもあるし。
逆に言えば、数学のない生き方しか選べないということだ。数学を知り、理解し、活用することで、コンピュータ、マーケティング、製品や建物の設計や製図、会計、天気予報など様々な分野で役立つ。仕事でなくても身近な出来事に数学を当てはめて、考えることも出来る。つまり人生の選択肢を広げて、豊かに生きることが出来るようになるのだ。
それに数学を学ぶことで、論理的な思考を養うことにも繋がるし、説明する能力も向上する。数字に基づいて根拠のある主張を行うことが出来る。数学の出来ない人間は表現力に乏しい。
ヒソヒソ・・・(いいネズミだと思うけど、1個いったら100個くらい言い返してくる。)
ピピピ・・・(学者気質なのデショウ。たぶん気持ちよくなって喋っているノデ、我慢して聞いてあげてクダサイ。)
私語はいかんと言っておろうが!同じ事を二度言わせんなッ!
余談
数学の説明で一番ダメなのは、一方的な説明になることだと思う。授業や講義なら聴講している学生に反応を見たり、問いかけたり出来るが、ブログではそれが難しい(コメントという形で反応は受け取れるが)。なので、今回はディスカッション形式で、「なぜ数学を学ぶのか」について書いてみた。
もちろんこの問いかけに対する答えは、いくらでもあるし、人によって違う。例えばパソコンを必要とする理由は人によって違う。大学のレポート作成、家で仕事をするため、ゲームなどの娯楽のため、それと数学が必要な理由は大して変わらない。
大事なのは自分の頭で思考し、自分なりの答えを見つけることだ。そのためには、検索エンジンで他人の答えを覗き見ても良いし、本でも参考になるものはいくらでもある。学んでから使い方を考えても良いし、使いたいことがあるから学ぶのも良い。
ただ理解出来ない、苦手だから使えないと言うのは、可能性を閉ざすだけだと知って欲しかった。